Calculo Multivariable: febrero 2022

COORDENADAS RECTANGULARES,CILÍNDRICAS Y ESFÉRICAS

📌 Sistema de coordenadas rectangulares

El sistema de coordenadas rectangulares (o plano cartesiano) es un objeto matemático formado por dos rectas perpendiculares trazadas sobre un plano llamadas "ejes", la recta horizontal es el eje X, la recta vertical es el eje Y. El plano queda dividido en cuatro partes llamados cuadrantes.

📌 Coordenadas cilíndricas

Los sistemas de coordenadas pueden ser definidos como formas de ubicar a puntos en el espacio. En el espacio tridimensional, el sistema de coordenadas cartesianas tiene la forma (x, y, z). Sin embargo, este sistema no siempre es el más conveniente, por lo que tenemos sistemas de coordenadas alternativos. Uno de estos sistemas es el sistema de coordenadas cilíndricas. Las coordenadas cilíndricas son consideradas como una extensión de las coordenadas polares hacia la tercera dimensión. La forma general de las coordenadas cilíndricas es (r, θ, z), en donde, r es la distancia desde el origen hasta el punto en el plano xy, θ es el ángulo formado con respecto al eje x y z es el mismo componente z que en coordenadas cartesianas.

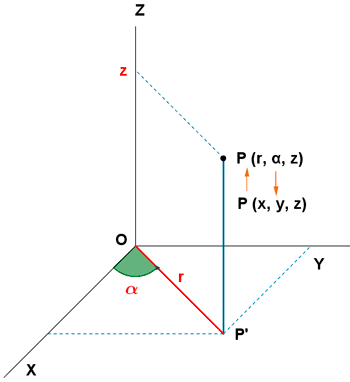
Relación entre coordenadas cilíndricas y cartesianas.

Para cambiar de coordenadas cilíndricas a cartesianas, se usan las fórmulas:

Para cambiar de coordenadas cartesianas a cilíndricas, se usan las fórmulas:

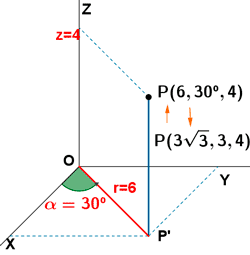
punto en coordenadas cilíndricas y cartesianas

Ejemplo 1:

El punto P(6, 30º, 4) está expresado en coordenadas cilíndricas. Halla sus coordenadas cartesianas.

punto en coordenadas cilíndricas y cartesianas

Ejemplo 2:

El punto P(-2, -2, 3) está expresado en coordenadas cartesianas. Halla sus coordenadas cilíndricas.

📌 Coordenadas esféricas

Un sistema de coordenadas es definido como una manera de definir y ubicar a un punto en el espacio. El sistema de coordenadas tridimensional más usado es el sistema cartesiano, el cual tiene la forma (x, y, z). Sin embargo, existen sistemas alternos que pueden resultar más convenientes dependiendo en la situación. Uno de estos sistemas es el sistema de coordenadas esféricas. Este sistema tiene la forma (ρ, θ, φ), en donde, ρ es a la distancia desde el origen hasta el punto, θ es el ángulo formado con respecto al eje x y φ es el ángulo formado con respecto al eje z.

Ejemplos de coordenadas esféricas

Para graficar a un punto que está representado en coordenadas esféricas, podemos empezar ubicándolo con respecto a su distancia desde el origen y su ángulo con respecto al eje x. Luego, lo ubicamos con respecto al ángulo que forma desde el eje z. El siguiente diagrama representa al punto $(3, \frac{\pi}{3}, \frac{\pi}{4})$ .

grafica de un punto en coordenadas esfericas

Podemos ver que, el ángulo φ es medido desde el eje z positivo. Este ángulo va desde 0 hasta π. Por otra parte, el ángulo θ no tiene ninguna restricción. Esto significa que en realidad, tenemos varias formas de representar a un punto en coordenadas esféricas. Esto se debe a que, si es que sumamos o restamos 2π o un múltiplo de 2π, obtenemos un ángulo equivalente. Por ejemplo, los ángulos $\frac{\pi}{3}, \frac{4\pi}{3}, \frac{2\pi}{3}$ son equivalentes.

Fórmulas de conversión de esféricas a cartesianas

Usemos el siguiente diagrama para derivar las fórmulas de conversión de coordenadas esféricas a coordenadas cartesianas:

coordenadas esfericas y coordenadas cartesianas

Podemos usar triángulos rectángulos y trigonometría para obtener ecuaciones para ρ, θ, φ en términos de x, y, z. La derivación de estas ecuaciones resulta más fácil si es que empezamos transformando de coordenadas esféricas a cilíndricas y luego, de coordenadas cilíndricas a cartesianas. Entonces, usamos el siguiente diagrama:

diagrma de coordenadas esfericas y cartesianas

Podemos encontrar a r y z usando la función seno y coseno respectivamente:

$z=\rho \cos(\phi)$

$r=\rho \sin(\phi)$

El tercer componente aquí es $\theta$ . Ahora, usamos las fórmulas de transformación de coordenadas cilíndricas a cartesianas:

$x=r~\cos(\theta)$

$y=r~\sin(\theta)$

$z=z~~~~~$

Si es que usamos estos dos conjuntos de ecuaciones, tenemos:

$x=\rho \sin(\phi)\cos(\theta)$

$y=\rho \sin(\phi)\sin(\theta)$

$z=\rho \cos(\phi)~~$

EJERCICIO 1

Si es que tenemos las coordenadas esféricas $(3, \frac{2\pi}{3}, \frac{\pi}{4})$ , ¿Cuál es su equivalente en coordenadas cartesianas?

Solución

Podemos observar los valores $\rho=3,~\theta=\frac{2\pi}{3},~\phi=\frac{\pi}{4}$ . Usamos los valores junto con las fórmulas vistas arriba para encontrar el valor de x:

$x=\rho~\sin(\phi)\cos(\theta)$

$x=3~\sin(\frac{\pi}{4})\cos(\frac{2\pi}{3})$

$x=-1.06$

El valor de y es:

$y=\rho~\sin(\phi)\sin(\theta)$

$y=3~\sin(\frac{\pi}{4})\sin(\frac{2\pi}{3})$

$y=1.84$

El valor de z es:

$z=\rho~\cos(\phi)$

$z=3~\cos(\frac{\pi}{4})$

$z=2.12$

Las coordenadas cartesianas del punto son (-1.06, 1.84, 2.12).

EJERCICIO 2

Tenemos las coordenadas esféricas $(6, \frac{5\pi}{3}, \frac{\pi}{2})$ . ¿Cuál es su equivalente en coordenadas cartesianas?

Solución

Podemos extraer los valores $\rho=6,~\theta=\frac{5\pi}{3},~\phi=\frac{\pi}{2}$ . Entonces, usamos las fórmulas junto con estos valores para encontrar el valor de x:

$x=\rho~\sin(\phi)\cos(\theta)$

$x=6~\sin(\frac{\pi}{2})\cos(\frac{5\pi}{3})$

$x=3$

El valor de y es:

$y=\rho~\sin(\phi)\sin(\theta)$

$y=6~\sin(\frac{\pi}{2})\sin(\frac{5\pi}{3})$

$y=-5.2$

El valor de z es:

$z=\rho~\cos(\phi)$

$z=6~\cos(\frac{\pi}{2})$

$z=0$

Las coordenadas cartesianas del punto son (3, -5.2, 0).

Fórmulas de conversión de cartesianas a esféricas

Para derivar las fórmulas de conversión de coordenadas cartesianas a coordenadas esféricas, usamos el mismo diagrama:
coordenadas esfericas y coordenadas cartesianas

El componente ρ puede ser encontrado en términos de x, y, z usando el teorema de Pitágoras en tres dimensiones. Entonces, tenemos:

${{\rho}^2}={{x}^2}+{{y}^2}+{{z}^2}$

$\rho=\sqrt{{{x}^2}+{{y}^2}+{{z}^2}}$

El ángulo θ es encontrado usando el mismo proceso de coordenadas cilíndricas. Usamos a la tangente inversa, en donde, y es el lado opuesto del ángulo y x es el lado adyacente. Entonces, tenemos:

$\theta={{\tan}^{-1}(\frac{y}{x})$

Algo que debemos considerar es que, muchas veces el ángulo dado por la calculadora no es el correcto. Esto es debido a que la función tangente inversa tiene un rango que va desde $-\frac{\pi}{2}$ hasta $\frac{\pi}{2}$ , por lo que no cubre los cuatro cuadrantes. Para corregir esto, sumamos 180° o π si es que el punto está en el segundo o tercer cuadrante y sumamos 360° o 2π si es que el punto está en el cuarto cuadrante. Si es que el punto está en el primer cuadrante, el valor dado por la calculadora sí es correcto.

Para encontrar al ángulo φ, podemos usar la función coseno. Vemos que el lado adyacente a este ángulo es el lado z y la hipotenusa es igual a ρ. Entonces, tenemos:

$\phi={{\cos}^{-1}}(\frac{z}{\rho})$

diagrma de coordenadas esfericas y cartesianas

EJERCICIO 1

El punto (2, 3, 4) está escrito en coordenadas cartesianas. ¿Cuál es su equivalente en coordenadas esféricas?

Solución

Podemos observar los valores $x=2, ~y=3,~z=4$ . Encontramos los valores de ρ, θ y φ, usando las fórmulas derivadas. Entonces, el valor de ρ es:

$\rho=\sqrt{{{x}^2}+{{y}^2}+{{z}^2}}$

$\rho=\sqrt{{{2}^2}+{{3}^2}+{{4}^2}}$

$\rho=\sqrt{4+9+16}$

$\rho=\sqrt{29}$

$\rho=5.39$

Ahora, usamos la tangente inversa para encontrar a θ:

$\theta={{\tan}^{-1}}(\frac{y}{x})$

$\theta={{\tan}^{-1}}(\frac{3}{2})$

$\theta=0.98$ rad

Este valor es el correcto ya que el punto está en el primer cuadrante (los valores de x y y son positivos).

Usamos al coseno inverso para encontrar el valor de φ, :

$\phi={{\cos}^{-1}}(\frac{z}{\rho})$

$\phi={{\cos}^{-1}}(\frac{4}{5.39})$

$\phi=0.73$ rad

Las coordenadas esféricas del punto son (5.39, 0.98 rad, 0.73 rad).

EJERCICIO 2

Si es que el punto (-2, -4, 5) está en coordenadas cartesianas, ¿cuál es su equivalencia en coordenadas polares?

Solución

Tenemos los valores $x=-2, ~y=-4,~z=5$ . Usamos las ecuaciones obtenidas junto con estos valores para encontrar las coordenadas esféricas. El valor de ρ es:

$\rho=\sqrt{{{x}^2}+{{y}^2}+{{z}^2}}$

$\rho=\sqrt{{{(-2)}^2}+{{(-4)}^2}+{{5}^2}}$

$\rho=\sqrt{4+16+25}$

$\rho=\sqrt{45}$

$\rho=6.71$

El valor de θ es:

$\theta={{\tan}^{-1}}(\frac{y}{x})$

$\theta={{\tan}^{-1}}(\frac{-4}{-2})$

$\theta=1.11$ rad

En este caso, tanto el componente x como el componente y son negativos. Esto significa que el punto se ubica en el tercer cuadrante y tenemos que sumar 180° o π para obtener el ángulo correcto. Entonces, el ángulo correcto es $\theta=1.11+\pi=4.25$ rad.